11.线性排序案例
目录介绍
- 01.先看一下思考题
- 02.桶排序(Bucket sort)
- 03.计数排序(Counting sort)
- 04.基数排序(Radix sort)
01.先看一下思考题
- 本节讲三种时间复杂度是O(n)的排序算法:桶排序、计数排序、基数排序。因为这些排序的时间复杂度是线性的,所以我们把这类排序算法叫作线性排序(Linear sort)。这三个算法不涉及元素之间的比较操作,是非基于比较的排序算法。
- 先给出一道思考题:**如何根据年龄给100万用户排序?**你可能会说,用上一节讲的归并、快排就可以搞定啊!是的,它们也可能完成功能,但是时间复杂度最低也是O(nlogn)。有没有更快的排序方法呢?让我们一起进入今天的内容!
02.桶排序(Bucket sort)
2.1 桶排序的核心思想
- 桶排放的核心思想是,将要排序的数据分到几个有序的桶里,每个桶里的数据再单独进行排序。桶内排序之后,再把每个桶里的数据依次取出,组成的序列就是有序的了。

image
2.2 桶排序复杂度
- 桶排序的时间复杂度为什么是O(n) 呢?
- 如果要排序的数据有n 个,我们将其均分到 m 个桶内,每个桶里就有 k = n/m 个元素。
- 每个桶内部使用快速排序,时间复杂度为O(klogk)。
- m个桶排序的时间复杂度就是 O(mklogk),把 k = n/m 代入可得时间复杂度为O(nlog(n/m))。
- 当桶的个数m接近数据个数n时,log(n/m)就是一个非常小的常量。这时候桶排序的时间复杂度就接近于O(n)。
- 桶排序看起来很优秀,那它是不是可以代替我们之前讲的排序算法呢?
- 当然是不可以的。桶排序对要排序的数据的要求是非常苛刻的。
- 首先,要排序的数据需要很容易能划分到 m 个桶,并且,桶与桶之间有着天然的大小顺序。这样每个桶内的数据排序完之后,桶与桶之间就不需要再进行排序了。
- 其次,数据在各个桶之间分布是比较均匀的。如果数据经过桶的划分之后,有些桶的数据非常多,有些非常少,很不均匀,那桶内排序的时间复杂度就不是常量级了。极端情况一,如果数据都被划分到一个桶里,那就退化成O(nlogn)的排序算法了。
2.3 桶排序使用场景
- 桶排序比较适合用在外部排序中。
- 所谓的外部排序就是数据存储在外部磁盘中,数据量比较大,内存有限,无法将数据全部加载到内存中。
- 举个例子
- 比如我们有10G 的订单数据,我们希望根据订单金额(假设金额过都是正整数)进行排序,但我们的内存有限,只有几百MB,没办法一次性把10GB 的数据加载到内存中,这个时候怎么办呢?
- 我们可以先扫描一遍文件,确定订单金额的数据范围。假定订单最小值是1元,最大值是10万元。把订单划分到100个桶里,第一个桶里订单金额的范围是1——1000,第二个桶的范围是1001——2000,依次类推。一个桶对应一个文件,文件编号从 00——99。
- 理想情况下,10GB的订单数据比较平均的分到100个文件中,每个文字里有约100MB的订单数据。然后把这100个文件依次放入内存中,用快排来排序。当所有文件里的订单数据排好序之后。再按照文件编号,从小到大把这100个的数据写入到一个文件中,可得到这10G订单排序好的数据了。
- 但数据不大可能均匀分布,若某个桶内的数据特别多,比如订单金额5001——6000的特别多,可以将这个区间的订单数据再细分到十个桶内(5001——5100,5101——5200……),其它的操作同上,就可以解决问题了。总之某个桶里的数据,内存放下下,就再细分。
03.计数排序(Counting sort)
3.1 什么是计数排序
- 当要排序的 n 个数据,所处的范围并不大时,比如最大值是k,就可以把数据分成 k 个桶。每个桶内的数据是相同的,省去了桶内排序的时间。
3.2 计数排序举例
- 就拿高考查分系统来说 ?当你查分数时,系统会显示出分数,及在省排名。假设该省50万考生,如何通过成绩快速排序得出名次?
- 考生满分是900分,最小是0分,这个数据的范围很小,所以可以分成901个桶,对应分数0到900分。根据考生的成绩,我们将50万考生划分到这901个桶里。桶内分数是一样的,不需要排序。依次遍历桶内的数据,放到一个数组中,就实现了50考生的排序。只涉及遍历操作,时间复杂度为O(n)。
- 计数排序算法的思想就这么简,和桶排序的方法类似,只是桶的粒度大小不一样。但它为什么叫计数排序呢?计数又体现在哪里?
- 为了方便说明,对数据规模做了简化。假设只有8个考生,分数在0到5分之间。假设这8个考生的分数在0到5之间。把这8个考生的成绩放入一个数组A[8]中,它们分别是:2,5,3,0,2,3,0,3.
- 考生的成绩从0到5分,我们使用大小为6的数组C[6]表示桶,其中下标对应分数。不过,C[6]内存储的并不是考生,而是对应的考生个数。像我们刚刚举的那个例子,我们只需要遍历一遍考生的分数,就可以得到C[6]的值
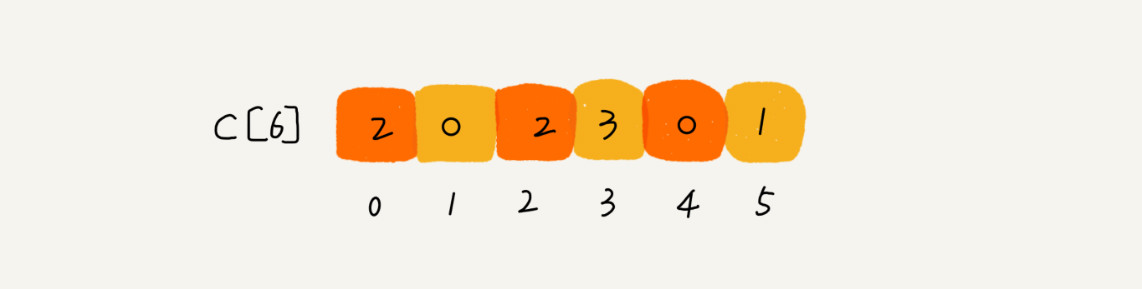
image
- 如图中所示,分数为3分考生有3个,小于3分的考生有4个,所以,成绩为3分的考生在排序之后的数组R[8],会保存下标4,5,6的位置
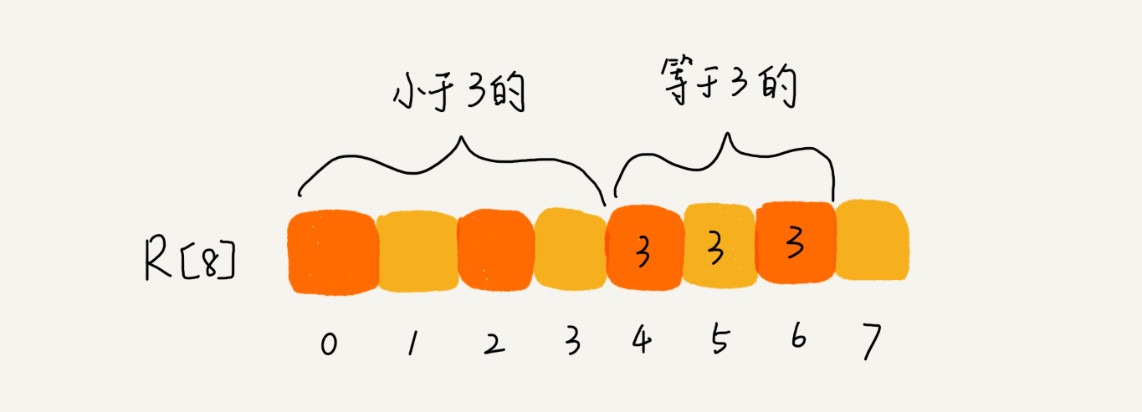
image
- 那我们如何快速计算出,每个分数的考生在有序数组中对应的存储位置呢?这个处理方非常巧妙,不容易想到。
- 思路是这样的:我们对C[6]数组顺序求和,C[6]存储的数据就变成了正面的样子。C[k]里存储小于等于分数k 的考生个数
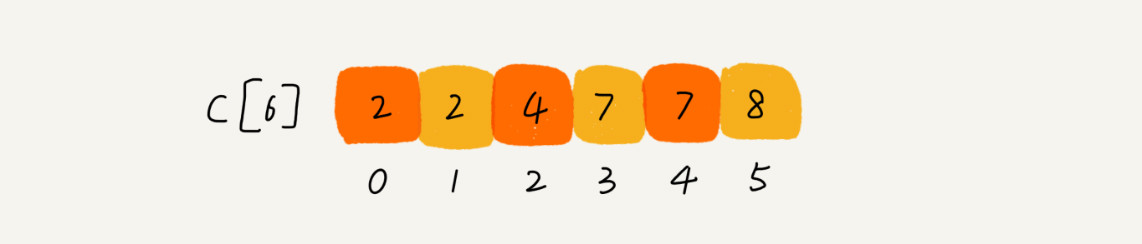
image
- 然后就进入比较难理解的部分。我们从后到前依次扫描数组A。比如,当扫描到 3 时,我们从数组C中取出下标为3的值7,也就是说,到目前为止,包括自己在内,分数小于等于3的考生有7个,也就是说3是数组R中的第7个元素。当3放入数组R后,小于等于3的元素只剩下6个了,所以相应的C[3]要减1,变成6。依次类推,当我们扫描到第2个分数为3的考生时,就会把它放入数组R中的第6个元素的位置。
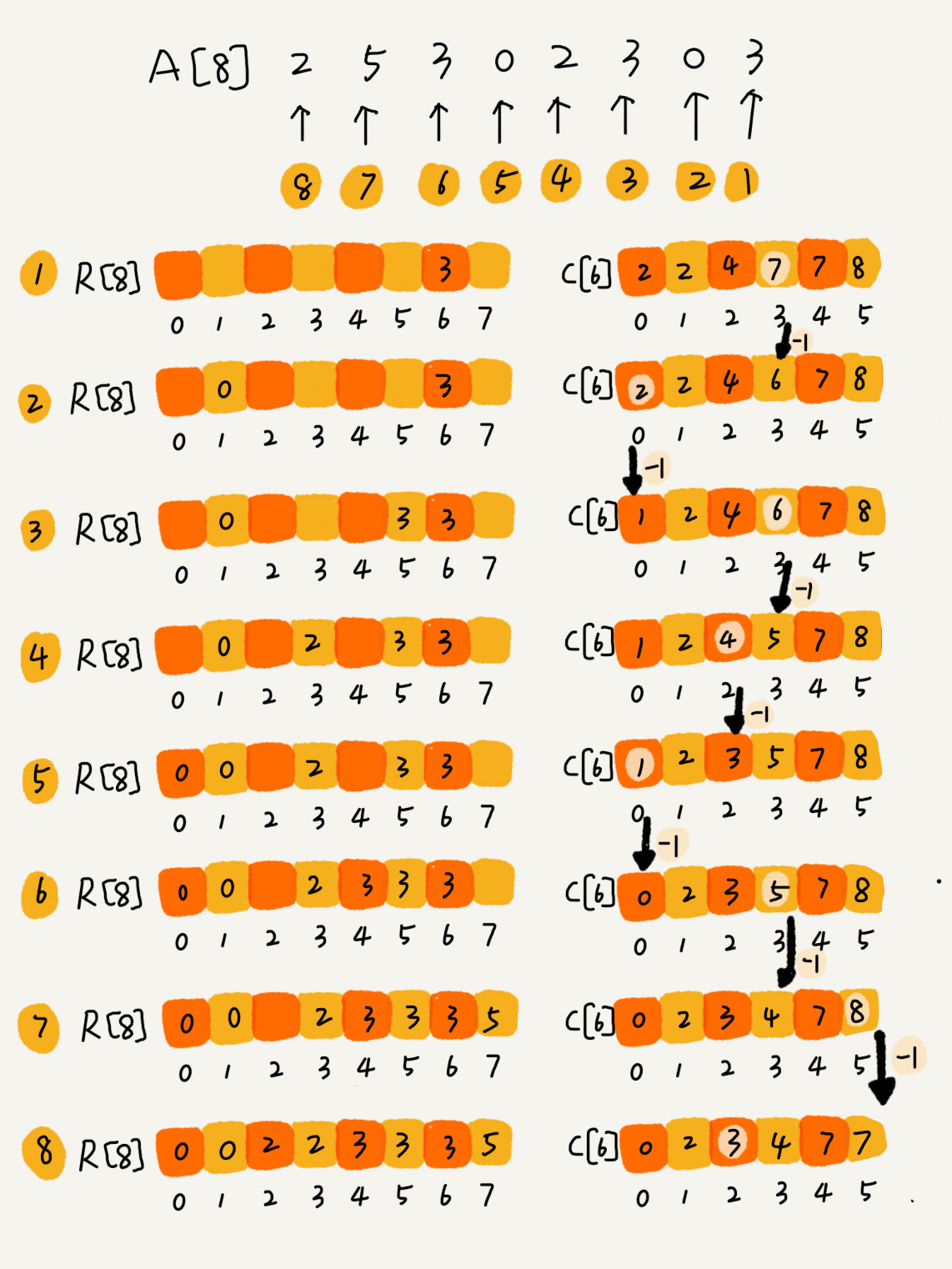
image
- 过程是有点复杂的,可以对照代码来看。
// 计数排序,a是数组,n是数组大小。假设数组中存储的都是非负整数。 public void countingSort(int[] a, int n) { if (n <= 1) return; // 查找数组中数据的范围 int max = a[0]; for (int i = 1; i < n; ++i) { if (max < a[i]) { max = a[i]; } } int[] c = new int[max + 1]; // 申请一个计数数组c,下标大小[0,max] for (int i = 0; i <= max; ++i) { c[i] = 0; } // 计算每个元素的个数,放入c中 for (int i = 0; i < n; ++i) { c[a[i]]++; } // 依次累加 for (int i = 1; i <= max; ++i) { c[i] = c[i-1] + c[i]; } // 临时数组r,存储排序之后的结果 int[] r = new int[n]; // 计算排序的关键步骤,有点难理解 for (int i = n - 1; i >= 0; --i) { int index = c[a[i]]-1; r[index] = a[i]; c[a[i]]--; } // 将结果拷贝给a数组 for (int i = 0; i < n; ++i) { a[i] = r[i]; } } - 这种利用另外一个数组来计数的实现方式是不是很巧妙呢?这也是为什么这种排序算法叫计数排序的原因。计数排序只能用在数据范围不大的场景,如果数据范围k比要排序的数据n在很多,就不适合用计数排序了。而且,只能用于非负整数排序,如果要排序的数据是其他类型,要将其在不改变大小的情况下,转化为非负整数
04.基数排序(Radix sort)
- 再来看这样一个排序问题。假设我们有10万个手机号码,希望将这10万个手机号码从小到大排序,你有什么比较快速的排序方法呢?
- 用之前说到的快排,时间复杂度可以做到O(nlogn),还有更高效的排序算法吗?
- 这个问题里有这样的规律:假设经比较两个电话号码a ,b 的大小,如果在前面几个位中,a手机号码已经比b 手机号码大了,那后面的几位就不用比较了。
- 借助稳定排序算法,这里有一个巧妙的实现思路。先按照最后一位来排序手机号码,然后,再按倒数第二们重新排序,以此类推,经过11次排序后,手机号码就都有序了。
- 简化数据,用这几个字母的例子来看图
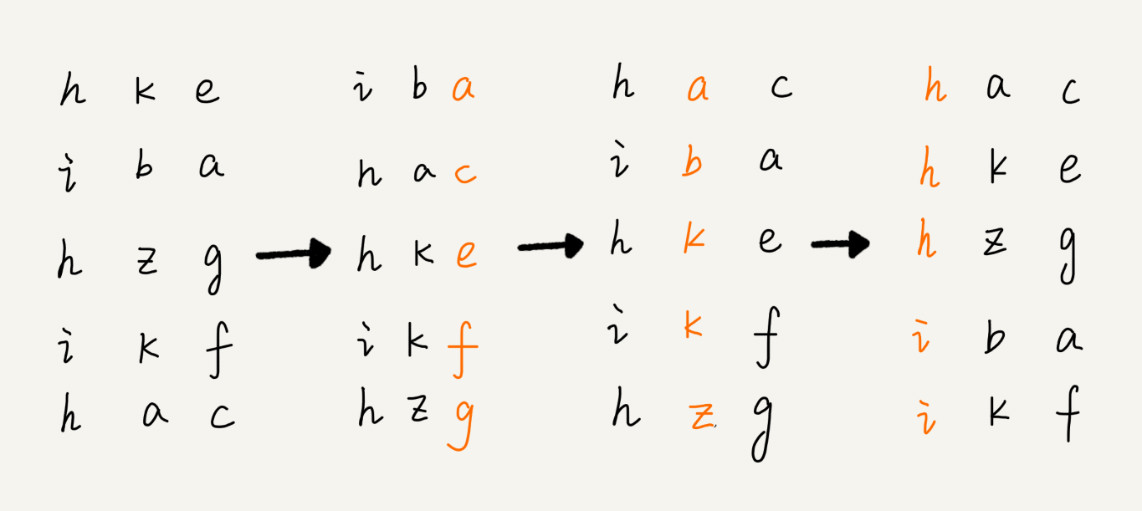
image
- 注意,这里按每位来排序的排序算法要是稳定的,否则这个思路就不正确了。
- 根据每位排序,可以用刚讲过的桶排序或者计数排序,时间复杂度可以做到O(n)。如果要排序的数据有k 位,就需要 k 次排序,总的时间复杂度就是O(kn)。当 k 不大的时候,比如手机号码的例子,是11位,O(kn)就近似等于O(n)。
- 总结下基数排序,它对要求排序的的数据是有要求的,需要可以分割出独立的“位”来比较,而且位之间有递进关系,如果 a 数据的高位比 b 数据大,那剩下的低位就不用比较了。除此之外,每一位的数据范围不能太大,要可以用线性排序算法来排序,否则,基数排序的时间复杂度就无法做到o(n)了。
